Гироскопический теодолит (гиротеодолит)

Гиротеодолит (рис. 1.80) используют для определения истинных азимутов направлений, в нем угломерный прибор соединен с датчиком направления меридианов. В качестве датчика обычно используют маятниковый гироскоп, который также называют гирокомпасом, указателем меридиана, гиробуссолью. Внутри гирокамеры 4 на тонкой металлической лен-точке-торсионе 8 подвешен чувствительный элемент 5 гироскопа. Гироскоп — трехфазный асинхронный двигатель, питается током по двум ленточным токопроводам 2 и торсионам.

Чувствительный элемент 5 помещен в корпус гироблока 7, который скреплен с алидадой угломерной части. При транспортировке прибора чувствительный элемент и корпус гироблока скреплен арретиром 6. При измерении наблюдают в окуляр автоколлиматора 1 на алидаде изображение штрихов его шкалы. Синхронно с движением по азимуту чувствительного элемента с помощью редуктора 3 поворачивается корпус гироблока, концы токопроводов и верхний зажим ленты, при этом исключается закручивани при движении чувствительного элемента.

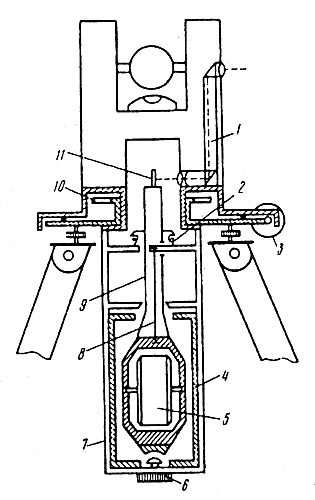
Рис. 1.80. Гиротеодолит

Для проектирования на горизотальный круг 10 точек реверсии колебаний чувствительного элемента и пользуют систему, состоящую из автоколлиматора 1 на алидаде и зеркала 1 укрепленного на штанге 9 чувствительного элемента.

В противоположных точках реверсии движение чувствительного эл мента прекращается, в момент остановки производят отсчеты по горизо тальному кругу через дополнительный окуляр, по отсчетам определяют значение N, соответствующее положению динамического равновесия чувств тельного элемента, при котором главная ось гироскопа совпадает с плоскостью истинного меридиана. После этого перекрестие нитей зрительной трубы наводят на визирную цель, азимут А направления на которую определяют. Значение

А=М - N + Δ,

где Δ - приборная поправка гиротеодолита, определяемая по ориентирован ному направлению с известным азимутом А, т. е. Δ = А - (М - N).

В геодезических построениях необходимо иметь дирекционные углы α, которые определяют по формуле

α = А — γ + ΔА + δ

где ΔА = (λ + L)sinφ — поправка за переход от астрономического азимута геодезическому (уравнение Лапласа), λ — астрономическая, a L — геодезическая долгота, φ — широта, γ — гауссово сближение меридианов, δ — поправка за кривизну геодезической линии на плоскости в проекции Гаусса-Крюгера, вычисляемая в сетях 3, 4-го классов или ниже по точности по формуле

δ₁₂ = -δ₂₁ = ƒ(х₂- х₁)y_m,

где ƒ =p"/2R2, для территории СНГ можно принять ƒ= 0,00253; у_m =0,5(у₁ +у₂) -среднее значение ординаты пунктов: с которого выполняют наблюдение и наблюдаемого. Значение у отсчитывается, как уже отмечалось, от осевого меридиана зоны со знаком плюс к востоку и со знаком минус — к западу от него. Если х_i, у_m, выражать в километрах, то δ получают в угловых секундах. При определении α с точностью 30" и ниже поправки ΔА и δ не вводят.