Расчет числа циклов искусственного искривления

Схема к расчету числа циклов искусственного искривления для увеличения интенсивности выполаживания скважины приведена на рис. 13.8. Задача состоит в том, чтобы определить на какой угол следует развернуть фактический профиль скважины С-1 в точке А, чтобы с учетом естественного выполаживания вывести скважину в точку D глубине Н (проектный профиль С-II).

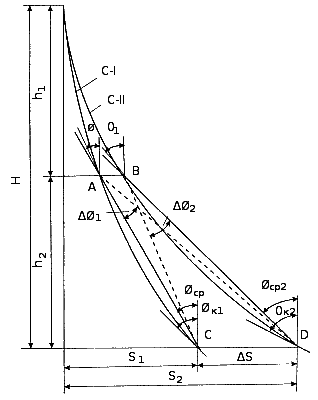Рис. 13.8. Схема к расчету необходимого угла отклонения скважины при ее внепроектном искривлении в вертикальной плоскости Последовательность расчета приводится ниже. Определяется кривизна Кθ1 и Кθ2 профилей скважины Кθ1 =(sinθ1-sinθ0)/h1,          (13.51) Кθ2 = (sinθ2 -sinθ0)/h1,             (13.52) где θ1 и θ2 - зенитные углы профилей соответственно фактической и проектной скважин; θ0 - начальный зенитный угол скважины; h1 - глубина замера зенитного угла (по вертикали). θ2 = arcsin(sinθ0 + K2h1).               (13.53) Определяется интенсивность искривления проектного iθ2 и фактического iθ1 профилей скважины: iθ1=Kθ157,3               (13.54) iθ2=Кθ257,3                 (13.55)

Вычисляются конечные зенитные углы проектного θ_k2, и фактического θ_k1 профилей скважины:

θ₁ = arcsin (sinθ₀ + К_θ1Н)               (13.56)
θ₂ = arcsin(sinθ₀ + К_θ2Н)               (13.57)

Определяются горизонтальные проекции проектного S₂ и фактического S₁ профилей скважины:

S₁ = (cosθ₀-cosθ_k1)/K_θ1.           (13.58)
S₂ =(cosθ₀-cosθ_k2)/K_θ2.                (13.59)

Определяется возможный отход забоев ΔS по горизонтали между проектным и фактическим профилями скважины

ΔS = S₂-S₁.                 (13.60)

Когда ΔS больше допустимого, расчеты продолжаются. Средний зенитный угол между точками А и С

θ_ср1=(θ₁-θ_k1)/2                (13.61)

Определяем длину отрезка АС

AC = h₂/cosθ_ср1              (13.62)

где h₂ - расстояние по вертикали между точкой замера зенитного угла и забоем проектной скважины.

Из Δ ADC по теореме косинусов

AD=√AC²+CD²-2AC∙CD∙cos(90º+θ_cp1)                         (13.63)

Из Δ ADC по теореме синусов

               (13.64)

Поскольку профиль скважины между точками А и D будет естественно выполаживаться, при расчете необходимого угла поворота траектории Δθ_и1 средствами искусственного искривления следует учесть естественное искривление:

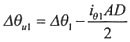(13.65)

Необходимое число циклов искусственного искривления n определяется исходя из величины отклонения скважины за цикл Δφ, взятой по паспорту отклонителя:

n=Δθ_и1/Δφ                   (13.66)

Ниже приводится расчет числа циклов искусственного искривления для «выкручивания» ствола скважины с использованием расчетной схемы приведенной на рис.13.8.

В данном случае фактическим является профиль С-II, проектным - С-I. Необходимо определить, на какой угол следует развернуть профиль скважины С-II в точке В, чтобы с учетом естественного выполаживания вывести скважину в точку С на глубине H.
Проводим первоначальные вычисления в той же последовательности, что и при выполаживании ствола скважины по формулам (13.51) -(13.60).

Средний зенитный угол между точками B и D.

θ_ср2=(θ₂+θ_к2)/2              (13.67)

Длина отрезка

BD = h₂ /cosθ_ср2           (13.68)

Из Δ CBD по теореме косинусов

BC=√CD2+BD2-2CD∙BD∙cos(90º-θcp2)             (13.69)

где CD=ΔS.

Из Δ CBD по теореме синусов

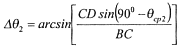                  (13.70)

Искусственное отклонение скважины С-II в точке В

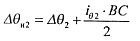                     (13.71)

Знак «+» перед дробью взят в связи с тем, что набранный угол Δθ₂ в процессе бурения будет уменьшаться за счет естественного выполаживания.

Необходимое число циклов искусственного искривления n вычисляем по формуле (13.66).

Ниже приведен пример расчета необходимого числа циклов искривления.

Пример 13.12. Определить угол, на который следует отклонить на глубине 300 м скважину, чтобы на глубине 800 м забой скважины привести в точку D если известно, что θ₀=5°; h₁=300м; h₂=500м; θ₁=8°; θ₂=11°.

Решение. По формуле (13.51) и (13.52) вычисляем кривизну проектного К_θ2 и фактического К_θ1 профилей скважины:

K_θ1 = (sin 8° - sin 5°)/ 300 = 0.0001745 м-1,
K_θ2 = (sin11° - sin 5°)/ 300 = 0,000349 м-1.

По формулам (13.54) и (13.55) находим интенсивность искривления проектного i_θ2 и фактического i_θ1 профилей скважины:

i_θ1= 0.0001745·57.3 = 0,01° / м,
i_θ2 = 0.000349·573 = 0.02° / м.

По формулам (13.56) и (13.57) определяем конечные зенитные углы проектного θ_k2 и фактического θ_k1 профилей скважины:
θ_k1= arcsin(sin 5° + 0,0001745·800) = 13,1°,

θ_k2 = arcsin(sin 5° + 0,000349·800) = 21.49°.

По формулам (13.58) и (13.59) вычисляем горизонтальные проекции проектного S₂ и фактического S₁ профилей скважины:

S₁ = (cos5°-cos 13,1°)/ 0.0001745 = 127.4 м,
S₂ = (cos 5°-cos 21.49°)/0.000349 = 188.3м.

По формуле (13.60) находим возможный отход забоев ΔS по горизонтали между проектным и фактическим профилями скважины

ΔS= 1883 -127,4 = 60,9 м.

По формуле (13.61) рассчитываем величину среднего зенитного угла между точками А и С

θ_ср1= (8,02 +13.10)/ 2 = 10,56°.

По формуле (13.62)

АС = 500/cos 10.56° = 508.6 м.

По формуле (13.63)

AD=√60,9²+508,6²-2∙60,9∙508,6∙cos(90º+10,56º)=523 м

По формуле (13.64)

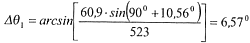
По формуле (13.65) определяем необходимый угол искусственного искривления скважины Δθ_и1 в точке А

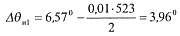
По формуле (13.66) находим необходимое число циклов искусственного искривления при Δφ=1,5°/цикл

n=3,96/1,5=2,7≈3цикла