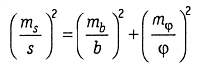Линейные измерения в полигонометрии 1 и 2-го разрядов / Параллактическая полигонометрия
Длины сторон в полигонометрии 1-го разряда измеряют с относительной погрешностью не более 1:10 000 малыми топографическими светодальномерами или подвесными мерными приборами.
Подвесными мерными приборами линии измеряют непосредственно путем многократного отложения проволоки или параллактическим способом, используя длину мерного прибора как постоянный параллактический базис.
В полигонометрии 2-го разряда стороны измеряют с относительной ошибкой не более 1:5000, разрешается применять оптические дальномеры, например Редта-002, обеспечивающие заданную точность.
Параллактический способ измерения линий, повышающий производительность труда по сравнению со способом непосредственного многократного отложения мерного прибора, заключается в построении базисной сети в виде параллактического звена с острыми углами, противолежащими короткому базису (рис. 1.9).
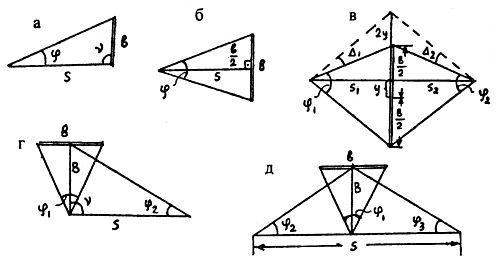
Рис. 1.9. Семы параллактических звеньев полигонометрии. а — звено треугольной формы; б — звено с симметричным расположением базиса относительно определяемой стороны; в — звено ромбической формы; г — сложное звено треугольной формы; д — сложное звено параллактической полигонометрии
Расстояние определяют тригонометрическим путём по точно измеренному малому базису и лежащему против него острому параллактическому углу и по измеренному с меньшей точностью прибазисному углу, который получается при пересечении базиса с определяемой линией.
В городских условиях и на строительных площадках в качестве базиса удобно применять двухметровые горизонтальные жезлы, изготавливаемые из инварного прута диаметром 8-12 мм, заключенного в дюралевую трубу диаметром 35-40 мм. Базисом является расстояние между визирными марками, укрепленными на концах инварного прута. Для установки жезла в горизонтальное положение используют круглый уровень, а в перпендикулярное к измеряемой линии — оптический визир.
Различные формы параллактических звеньев
Рассмотрим различные формы параллактических звеньев.
1. Звено треугольной формы (рис. 1.9, а). По теореме синусов
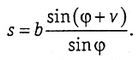
При v ≈ 90°, sin (φ+v) ≈ cosφ ≈1, sinφ≈; s≈b/φ; lns = lnb-lnφ