Для полной очистки забоя от разрушенной породы и выноса ее на поверхность расхода бурового раствора (подача насосов) Q должен обеспечивать такую скорость восходящего потока υв (в м/с), которая превышает скорость падения твердых частиц u (в м/с) при отсутствии движения жидкости под влиянием силы тяжести на величину желаемой скорости подъема w, т.е.
υв=u+w. (14.1)
В переходном и турбулентном режимах обтекания частицы (в м/с) вычисляется по формуле Риттингера.
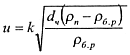 (14.2)
(14.2)
где k=√4g / 3kс - постоянная Риттингера; kс - коэффициент сопротивления движению, зависящий от конфигурации частицы, скорости ее обтекания и других факторов, для шара в среднем kc≈0,4); dч - диаметр самой крупной частицы, остающейся во взвешенном состоянии, определяемый по формуле
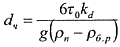 (14.3)
(14.3)
где τ0 - динамическое напряжение сдвига, Па; kd - экспериментальный коэффициент, значения которого зависят от диаметра (рис. 14.1).
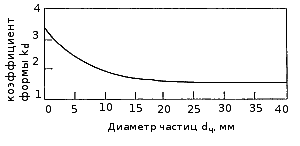 |
Рис.14.1. Значения коэффициента формы kd, введенного Р.И.Шищенко На практике в формулу (14.3.) вместо τ0 часто подставляют СНС (θ), так как многие буровые растворы не подчиняются модели вязкопластичной жидкости во всей области и изменения градиентов скоростей. |
Для частиц неправильной формы используется эквивалентный диаметр сферы.
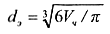 (14.4)
(14.4)
где Vч = πd3ч/6.
Для определения расчетного диаметра частиц породы, выбуриваемых шарошечным долотом можно воспользоваться выражением
dч=0,56√(l-b)h (14.5)
где l - максимальный шаг зубьев в плоскости забоя; b - ширина зубьев в плоскости забоя; h - высота зубьев.
При наличии обломков породы со стенок скважины в качестве расчетного диаметра dч можно принять величину кольцевого зазора между стенкой скважины и муфтой бурильных труб.
При использовании алмазных долот частицы выбуренной породы сравнительно мелкие и их вынос на поверхность не вызывает затруднении.
|
|
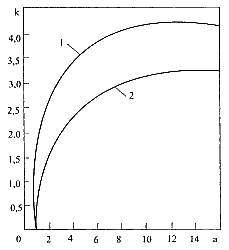
Значение k = √4g/3кс можно определить из графика (рис. 14.2) в зависимости от параметра a=dч/d0. (14.6) где d0 - диаметр наибольшей частицы, оставшейся во взвешенном состоянии. Рис. 14.2. Изменение коэффициента k в формуле Риттингера, по Р.И.Шищенко: 1 - сфера; 2 - плоская частица. При а<3 режим обтекания частицы ламинарный; при 3≤а≤7 - переходный и при а>1 - турбулентный. Для частиц бурового шлама скорость проскальзывания принимается равной 0,3-0,4 аналогичной скорости для сферы. При ламинарном режиме
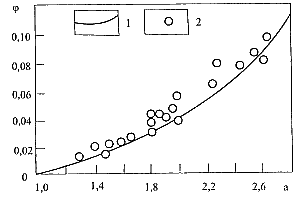
где n - пластическая вязкость. Па·с; ψ(a) - экспериментальная функция, график которой приведен на рис. 14.3. Рис.14.3. Изменение фукции ψ(a), введенной Р.И.Шищенко: 1, 2 - теоретические и экспериментальные данные соответственно |
Требуемую скорость подъема частиц шлама w можно определить из выражения
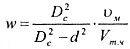 (14.8)
(14.8)
где Dc - диаметр скважины; d - наружный диаметр бурильных труб; υм - скорость проходки; Vт.ч - объемная доля твердых частиц.
Допускаемая максимальная доля объема шлама, при превышении которой возникает опасность образования сальников и прихватов, в практических расчетах принимается Vт.ч=5% (уменьшается до 2 %, если буровым раствором служит вода или другие легкие жидкости пониженной вязкости).
Для практических расчетов скорость выноса частицы w принимается
равной (0,1÷0,3)u и тем больше, чем глубже скважина и выше
vм.
Определив скорость vв необходимую для
транспортирования шлама к устью скважины, можно вычислить требуемый расход
бурового раствора (в м3/с), обеспечивающий вынос частиц разбуриваемой породы
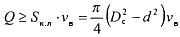 (14.8, a)
(14.8, a)
где Sк.п - площадь сечения кольцевого пространства между стенками скважины и бурильных труб, м2.
Полученное по формуле (14.8,а) значение Q уточняется проверкой условия, обеспечивающего очистку забоя скважины от шлама
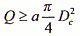 (14.8,б),
(14.8,б),
где а=0,35÷0,5 м/с при роторном способе и бурении электробурами; а=0,5÷0,7 м/с при бурении гидравлическими забойными двигателями.
Если форма частиц шлама близка к правильному многограннику, то минимально необходимое значение расхода Qmin (в м3/с) при ламинарном режиме течения бурового раствора, обеспечивающее качественную очистку ствола скважины, можно определить из выражения
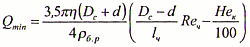 (14.10)
(14.10)
где η - пластическая (или структурная) вязкость, Па·с; lч - характерный размер частицы шлама, м; Rеч - число (параметр) Рейнольдса, характеризующее режим обтекания частицы средой.
Reч = Ar*/(18 /а1 + 0.61√Ar*/а2); (14.11)
Нек - число Хедстрема для кольцевого сечения,
Нек=τ0ρб.р (Dc-d)2/η2 (14.12)
Ar*=Ar-6Heч (14.13)
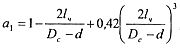 (14.14)
(14.14)
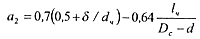 (14.15)
(14.15)
Ar - параметр Архимеда; Неч - параметры Хедстрема для частицы; а1 - коэффициент влияния формы частицы и стенок канала при ламинарном обтекании; а2 — коэффициент влияния формы и стенок канала при турбулентном обтекании; δ, dч - соответственно высота и диаметр частицы (если форма частиц близка к правильному многограннику, то δ,dч=l).
Параметр Архимеда
Ar=qρб.рl3ч(ρч-ρб.р )/η2 (14.16)
Нек=τ0ρб.р l2ч /η2 (14.17)
Параметр Reч, вычисленный по формуле (14.11), сравнивается с критическим параметром
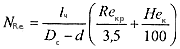 (14.18)
(14.18)
где Reкр - критическое значение параметра Рейнольдса, которое при Re*кp =1600 вычисляется по формуле
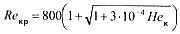 (14.19)
(14.19)
Если Reч<NRe, то качественная очистка ствола скважины возможна при ламинарном режиме течения бурвого раствора в затрубном пространстве скважины.
Пример 14.4. Определить минимальный расход бурового раствора при следующих исходных данных: Dc=190 мм; d=114 мм; параметры раствора: ρб.р=1300 кг/м3; τ0=4 Па; η=0,02 Па·с; характерный размер частиц шлама lч=0,01; форма частиц близка к правильному многограннику (т.е. δ/dч= 1); плотность частицы ρч=2300 кг/м3.
Решение. Параметры Аr и Неч, по формулам (14.16) и (14.17)
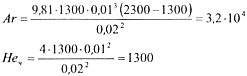
Определяются величины, входящие в выражение (14.11) [см.формулы (14.13), (14.14) и (14.15)]:
Аr* = 3,2·104-7800 = 2.4·104
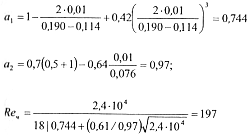
Параметр Хедстрема для кольцевого сечения по формуле (14.12)
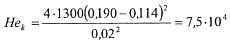
Критическое значение параметра Рейнольдса и критический параметр NRe :
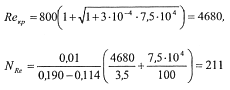
По формуле (14.10)
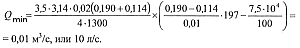
Скорость течения бурового раствора в затрубном пространстве составит
υ=0,01/0,018=0,55 м/с.

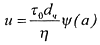 (14.7)
(14.7)