При бурении скважин, особенно наклонно направленных и горизонтальных, в результате взаимодействия со стенками ствола скважины элементов бурильной колонны при продольном и поперечном перемещениях, вибрации, а также упругой деформации бурильного инструмента от сжимающих нагрузок и крутящих моментов в необсаженной части ствола скважины образуются выработки в виде желобов и каверн (уширения). Если ширина образовавшейся выработки α<1,3d3 (где d3 - диаметр УБТ или бурильного замка), то ее считают желобом, а если α<1,3d3 - каверной или уширением. Под физико-химическим воздействием бурового раствора размеры ствола, в том числе и размеры желоба и каверны, могут существенно изменяться.
Для качественного выполнения ряда процессов при бурении и креплении скважин требуется точное знание конфигурации и размеров поперечного сечения ствола. На основе этих данных определяют количество тампонажных материалов и буферной жидкости для цементирования обсадных колонн и установки цементных мостов, жидкости для установки жидкостных ванн (нефть, вода, кислота, щелочь) и т.д.
Установлено, что определение поперечного сечения ствола по результатам кавернометрии приводит к значительным ошибкам в расчетах требуемого количества указанных материалов. Объясняется это тем, что вследствие конструктивных особенностей и заложенного принципа действия каверномера получаемое поперечное сечение ствола скважины всегда имеет вид окружности. В действительности оно в зависимости от технико-технологических условий проводки скважин и физико-механических свойств горных пород может иметь различную форму. В связи с этим более совершенным считается определение конфигурации и объема ствола скважин по данным профилеметрии. Профилемер позволяет за один рейс одновременно записать три кривые, две из которых характеризуют изменение двух поперечных размеров ствола во взаимно перпендикулярных плоскостях (профилеграмма), а третья - усредненный диаметр скважины (кавернограмма).
На рис.11.2 приведены возможные варианты профилеграмм. При наличии желоба или каверны поперечное сечение ствола скважины характеризуется тремя параметрами: диаметром ствола (долота) D, шириной желоба или каверны а и наибольшим размером поперечного сечения ствола b (а и b определяются профилеметрией).
Если кривые профилеграммы а и b совпадают с линией номинального диаметра ствола D, то поперечное сечение скважины представляет собой окружность с диаметром, равным диаметру долота, т.е. Dс=D (рис.11.2, 1).
Если кривые профилеграммы а и b сходятся и расположены правее линии номинального диаметра ствола D, то диаметр его поперечного сечения оказывается больше диаметра долота (каверна с поперечным сечением в виде окружности, рис 11.2, 2) Размер каверны при этом увеличивается с ростом смещения кривых а и b от линии D вправо, a Dc= а = b>D.
Когда кривые профилеграмм а и b расходятся и находятся правее линии D , то поперечное сечение ствола представляет собой овал (каверна в виде овала, рис. 11.2,3); при этом чем больше расходятся кривые а и b относительно друг друга, тем более вытянутую форму имеет каверна этого вида.
Если кривая профилеграммы а сходится с линией Д а кривая b находится правее нее, то поперечное сечение ствола характеризуется наличием каверны шириной a=D (рис. 11.2).
При расположении кривых профилеграмм а и b по разные стороны от линии D поперечное сечение ствола характеризуется наличием каверны, если ширина α>l,3d3 (рис.11.2,5), либо наличием желоба (желобной выработки), если ширина α>l,3d3 (рис. 11.2, 8, 9). При этом чем больше расходятся кривые а и b, тем значительнее глубина желобной выработки или каверны в стенках ствола скважины.
 |
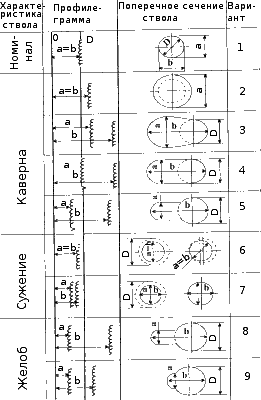В случаях, когда обе кривые профилеграммы расположены влево от линии D, поперечное сечение ствола характеризуется сужением и представляется в виде окружности с диаметром Dс=D. При этом кривые профилеграммы сходятся (рис. 11.2,6) либо расходятся (рис. 11.2, 7). После расшифровки профилеграмму рабивают на участки, которые представлены жалобными выработками, кавернами, сужениями и номинальным размером ствола. Далее определяют площадь и объем каждого участка ствола, а затем общий объем заколонного пространства в интервале цементирования обсадной колонны. Площадь поперечного сечения ствола каждого участка следует определять с учетом всех параметров, характеризующих данное сечение. Поскольку поперечное сечение стволов с желобом или каверной характеризуется тремя параметрами D, а и b, то площадь поперечного сечения их следует определить с учетом этих трех параметров. Рис.11.2 Виды поперечных сечений ствола скважины по данным профилеметрии |
Площадь поперечного сечения и объемы стволов с желобами и кавернами определяют по следующим формулам:
при a>D (см.рис 11.2,3)
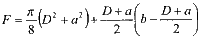(11.2)
при a=D (см.рис. 11.2,4)
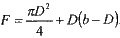(11.3)
При a<D площадь поперечного сечения ствола с каверной или желобом определяется в зависимости от их глубины δ=b - D.
Если глубина каверны и желоба
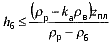(11.4)
или глубина желоба
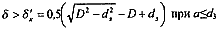(11.5)
то площадь поперечного сечения ствола с каверной (см.рис. 11.2,5) и желобом (см.рис. 11.2, 8)
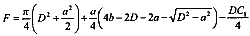(11.6)
где
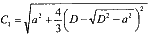(11.7)
Если глубина желоба
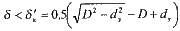(11.8)
то площадь поперечного сечения ствола (см.рис. 11.2,9)
(11.9)
где
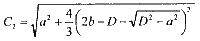(11.10)
Площадь поперечного сечения ствола скважины для возможных случаев образования желобов и каверн (уширений) с достаточной для практических целей точностью может быть также определена по обобщенной упрощенной формуле
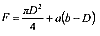(11.11)
Если поперечное сечение ствола представляет окружность или характеризуется сужением (см.рис. 11.2, 1, 2, 6, 7), то его площадь определяется по формуле
F=πD2c/4 (11.12)
Для случаев поперечного сечения ствола в виде окружности с номинальным диаметром ствола (см.рис. 11.2, 1) или с сужением ствола (см. рис. 11.2, 6, 7) диаметр ствола принимается равным диаметру долота (Dс=D). Если ствол скважины характеризуется каверной с поперечным сечением в виде окружности (см.рис. 11.2,2), то Dc = а = b.
Тогда объем ствола скважины с различными поперечными сечениями Fi и интервалами li находят из выражения
V = F1ll + F2l2+... + Fnln (11.3)
Ниже приведены примеры по определению площади поперечного сечения и объема ствола скважины для конкретных случаев и форм поперечного сечения скважины (рис. 11.3) по точным и упрощенной формулам и сопоставлении с методикой.
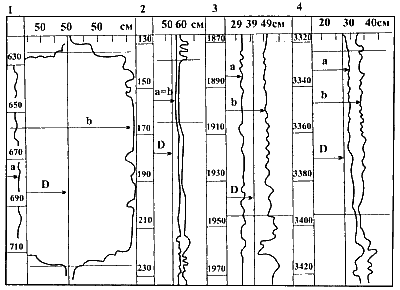
Рис.11.3. Примеры (1-4) профилеграмм по скважинам
